Zadanie z rachunku prawdopodobieństwa

Zadanie, które chcę zadać osobom mającym styczność z matematyką brzmi następująco:

Pragnę obliczyć prawdopodobieństwo wylosowania konkretnej liczby ze zbioru n-elementowego w k-losowaniach. Jaki jest wzór na takie obliczenia? Warunkiem jest by warianty (a,b) i (b,a) nie były potraktowane jako ten sam wariant oraz by w obliczeniach wariant (b,b) nie był uwzględniany w wyniku.

Mam nadzieję, że jest to zrozumiałe.

Wersja dla RPG'owców:
Poszukuje tablic prawdopodobieństwa dla k10, a dobrze by było też mieć wzór pozwalaący na takie obliczenia wrazie potrzeby.

Udało mi się sklecić coś takiego:

{[1-(a/b)]^c}*100

a - liczba oczekiwanych oczek na kości
b - zakres wyników
c - liczba rzucanych kości

Szansa wyrzucenia 6 lub więcej na jednej kości:

{[1-(5/10)]^1}=50%

Szansa wyrzucenia 8 lub więcej na siedmiu kościach
{[1-(7/10)]^7}*100%=
[(1-0.7)^7]*100%=
(0.3^7)*100%=
0,0002187*100%=
2,2%

Szansa wyrzucenia przynajmniej jednej 6 na dwóch kościach:
|[(5/10^2)-1]|*100%=
|(0.25-1)|*100%=
75*100%=
75%

EDIT:

Cytat:

Poszukuje tablic prawdopodobieństwa dla k10, a dobrze by było też mieć wzór pozwalaący na takie obliczenia wrazie potrzeby.

Proszę:
0 - 10%
1 - 10%
2 - 10%
3 - 10%
4 - 10%
5 - 10%
6 - 10%
7 - 10%
8 - 10%
9 - 10%

Wzór: 1/dx
dx - ilość ścianek na kości.

A tak na poważne w tym edicie: zależy Rapo o jaką tablicę prawdopodobieństwa Ci chodzi. Ja na przykład podałem Ci taką tablicę ale jak się domyślam - chodzi Ci o coś innego. Niestety nie wiem o co.
Piszesz o losowaniu "konkretnej liczby". To zagadka - nie wiem czy zamierzasz wyniki na kości(ach) mnożyć, dodawać czy odejmować. Czy zamierzasz bawić się L5K czy WoD, a może Q10. Itd, itp.

Tak mi się zdawało, że będzie niezrozumiałe, bo sam nie byłem pewien jakich słów użyć.

nWoD

k10\ s*| 1 | 2 | 3
______|_______|_______|_____
1 | 30% | - | -
2 | 42% | 9% | -
3 | 44,1% | 18,9% | 2,7%

*sukces - ilość wyników z przedziału 8-10

Przykład:
rzut 3k10. uzyskano wyniki 8,3,7 - Prawdopodobieństwo 1 sukcesu wynosiło 44,1%
rzut 2k10. uzyskano wyniki 9,8 - Prawdopodobieństwo 2 sukcesów wynosiło 9%

Wzór którego szukam pozwolił by na zmianę wielkości zbioru (typu kości) i liczby lsowań (ilości kości którymi wynywany jest rzut).

Mam nadzieję że to rozjaśniło sytuację.

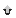Wykorzystaj schemat Bernoulliego.

k - ilość sukcesów
N - ilość prób
p - prawdopodobieństwo sukcesu w jednej próbie
q - prawdopodobieństwo porażki w jednej próbie

Przykład: wspomniany przez Ciebie rzut 3d10, szansa jednego sukcesu:

Jestem zobowiązany. Z tym wzorem już gdzieś się spotkałem w trakcie moich poszukiwań, ale niebyło tam instrukcji obsługi.

Co mnie zaskoczyło to fakt, że jest to permutacja - byłem święcie przekonany, że potrzebuje czegoś z wariacji. Zbyd długo bez matmy. Chyba w wakacje odświerzę braki.

Jeszcze raz dziękuję.